Cross-validation on the wine dataset

In this post, we will learn about cross-validation which is different from the simpler train_test validation technique that we know from earlier where we split the data into two sets of 80%-20%, or 70%-30% ratios. This simple train_test approach has several downsides namely:

Since train and test sets are split randomly, we risk losing data to train our model for effective performance, the more data for training the better our model
We don't know the effective split ratio of train-test split and always need to rely on experimentation
The test set may not be representative of the entire data and can give us misleading evaluation scores.

Now we will learn about k-fold cross validation. We will do a two-step splitting now.

We separate the entire data into train_test portions of our desired ratio and call it train and validation sets.
Then we will split the train set equally k times. Say k=5, so we will split our original data into 5 portions. These portions are called folds.
After doing so, we will consider one of those folds as test here and the rest of the 4 portions as train sets. We will perform training like this and then repeat the same process k times each time choosing a different fold as the test set. Here is a picture illustrating this concept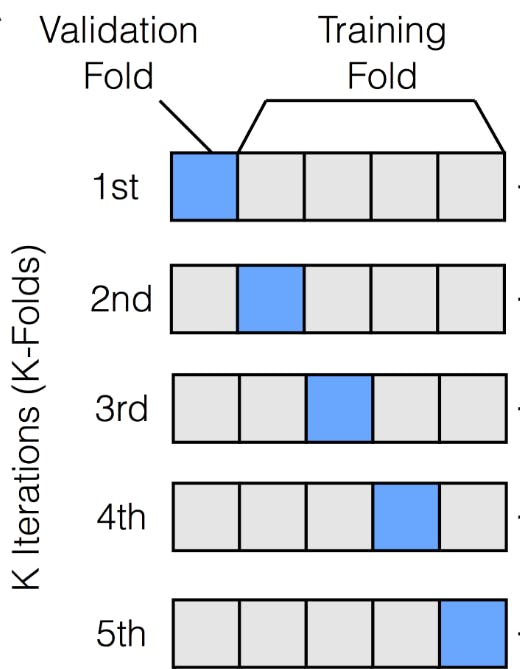 After doing so, we average the errors to get an overall measure of error.

Let's see how this works in action in code.

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

from sklearn.datasets import load_wine

data = load_wine()
wine_data = pd.DataFrame(data.data, columns=data.feature_names)
wine_target = pd.DataFrame(data.target, columns=['wine_class'])
wine_data.head()

Here's a quick peek at the dataset

Since the goal of this post is to learn about cross-validation I will skip other pre-processing, EDA, and feature selection tasks on the dataset. In practical situations, you don't want to skip these steps though. Let's cross-validate now.

We will leave out a portion of the dataset for final validation, just to make sure everything worked fine. We will do so by simply splitting the data into train and test sets where we will perform cross-validation only on the training set and leave out the test set for our said validation.

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
    wine_data, wine_target, test_size=0.2, random_state=0)

Now we will only cross-validate on the train sets. Let's see how that works.

from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=5)

from sklearn.model_selection import cross_val_score
scores = cross_val_score(knn, X_train, y_train, cv=5)

Scikit-learn has an amazingly intuitive interface for everything. Here we are instantiating a KNeighbors classifier object with hyperparameter number of neighbors to 5. We previously found this value to be optimal by doing a simple GridSearch here. Then we are passing the classifier, training data, and the number of folds, cv=5 to the cross_val_score object. Then scikit-learn will perform cross-validation steps 5 times as we learned above. So we get 5 scores of each folds like so,

array([0.68965517, 0.65517241, 0.64285714, 0.75 , 0.67857143])

Now we will validate the score on the validation set that we held out before doing any cross-validation.

from sklearn import metrics
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)

metrics.accuracy_score(y_test, y_pred)

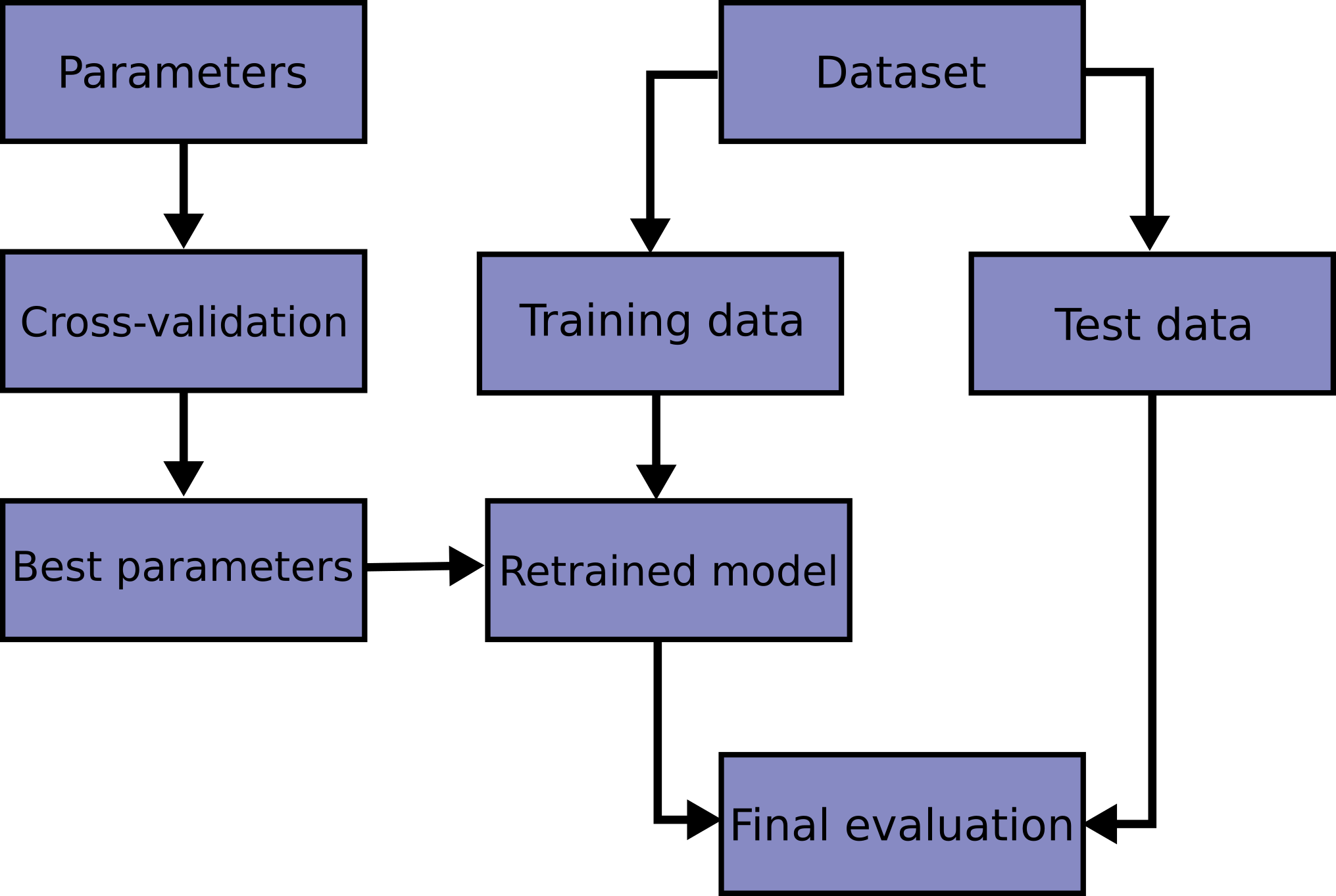
We get a score of 80% which looks great. However, you should be a bit cautious about using cross-validation with large datasets and iterating k times k-1 data points would be approximately O(k^2) which would get really slow and be resource-intensive. Finally, cross-validation is part of a larger ML workflow as shown by the scikit-learn docs In the next post, we will learn how to do GridSearch and RandomSearch utilizing CV to find the best combination of hyperparameters.

References

Scikit-learn docs